[統合的運動生成概念]
角運動量保存則について
みなさま,おつかれさまです,舟波真一です。
コラムで統合的運動生成概念,本日は「角運動量保存則」について考えていきます。
角運動とは回転運動であり,角運動量とは,等速回転運動をしている物体の慣性モーメント(I)と角速度(ω)の積で表されます。
慣性モーメント(I)とは,回転する物体の質量(m)と回転半径(r)の2乗の積で求めることができ(I=mr2),慣性モーメントが高いと,回転させづらく,一旦回転しだすと止めづらくなる物体となります。
大きなコマと小さなコマを想像して頂ければお判りだと思います。
大きなコマは,小さなコマとくらべて,回転させにくいですが,いったん回ってしまうと小さなコマより長く回転できます。つまり,止まりにくい物体となります。
ですので,慣性モーメントが高い物体は,扱いにくい物体であるといえます。
したがって,角運動量(L)=I×ωという公式が成立します。
質量が大きいほど,回転半径が大きいほど,角速度が速いほど,角運動量は増大することになります。
膝関節の伸展という角運動を例に上げますと,
膝関節が回転中心となり,膝関節から下腿・足部の質量中心点までが半径となります。
膝関節を伸展させることで角運動が起こり,膝関節が1秒間に伸展する角度が角速度となります。
単位は(rad/s)ラジアンというものになります。
歩行の遊脚の例では,膝関節屈曲位と膝関節伸展位での振り出しを比較すると,
膝関節伸展位での振り出しでは回転半径が増大することで,慣性モーメントも増大します。
そのため振り出し始めや振り出しを制動するのに大きなエネルギーが必要となるのです。
たとえば,長下肢装具などで膝関節を伸展固定して歩こうとすれば,
回転半径がおおきくなりますので,慣性モーメントが大きくなり,とても扱いにくい物体になるという事になります。
膝関節は曲がったほうがいいですよね。
では,この角運動量が保存されるとは,どういうことなのでしょうか?
角運動量保存則は外力が働かなければ,角運動量は一定に保たれるという法則です。
ニュートン力学の第一法則である,慣性の法則に基づきます。
角運動量保存則を説明するときにフィギュアスケートの例が解りやすいです。
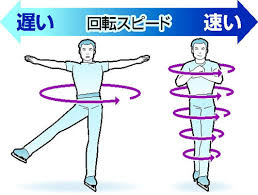
回転し始める時には筋活動により床反力を生成します。
その後,外力が働かない場合は,角運動量は一定に保たれ保存されることとなります。
回転してから両手を広げると回転半径が増大する分,回転速度は勝手に遅くなり角運動量が一定に保たれます。
また,両手を組んでしまうと,回転半径が減少する分,回転速度が勝手に速くなります。
いずれの運動も自動的に起こる事であり,角運動量保存則に従って生成されたものとなります。
身近な動作の中では,歩行を例にあげるとわかりやすいです。
立脚期では,骨盤の回旋に対して胸郭での反対側の回転が起こることにより,
身体を定位し歩行をおこなっています。
歩隔が狭くなるような歩行では,骨盤の回旋を増長させるために,
角運動量保存則に基づき相殺する胸郭の逆回転運動も増長することとなってしまうのです。
また,バレーボールのスパイクを例してみましょう。

スパイクを打つ瞬間ジャンプをし,胸郭を回旋させボールを打とうとしますが,
その際,胸郭の回旋とは逆方向に骨盤は動きます。
これにより2つの角運動量を相殺するための運動が起こることで身体を定位させ,
安定した動作となり,身体では角運動量は保存されます。
また上半身の後方への回転に対して,下半身の回転が逆に生成されています。
仮に膝伸展位になった場合,下半身の回転半径が大きくなり,慣性モーメントが増大します。
すると上半身の逆回転は,速度を速めるか過緊張で固めて回転半径を増大させるかの,
いずれかが必要となります。
いずれの場合もパフォーマンスの低下を招き,
2つの回転の軸となった腰部付近には過剰運動のストレスが発生することになってしまうのです。
このように,床反力を受けない動作においては角運動量保存則に従う割合は大変大きくなります。
角運動量保存則は,すべての動作で共通する法則であり,
この一連の運動は,物理的法則の基に起きてしまう運動で,普遍的なものなのです。
BiNI COMPLEX JAPAN 舟波真一でした。



